Скачать полный текст диссертации в формате PDF (2.9 Мб).
Глава 3. Метод прогнозирования на модели экстраполяции по выборке максимального подобия
3.1. Алгоритм экстраполяции временного ряда без учета внешних факторов
3.2. Алгоритм экстраполяции временного ряда с учетом внешних факторов
3.3. Алгоритм идентификации моделей
3.3.1. Описание алгоритма
3.3.2. Распараллеливание вычислений
3.3.3. Наборы моделей
3.3.4. Оценка времени идентификации
3.4. Алгоритм построения доверительного интервала
3.5. Выводы
3.1. Алгоритм экстраполяции временного ряда без учета внешних факторов
Метод прогнозирования на модели экстраполяции временных рядов по выборке максимального подобия содержит следующие алгоритмы.
1) Алгоритм экстраполяции временного ряда без учета внешних факторов.
2) Алгоритм экстраполяции временного ряда с учетом внешних факторов.
3) Алгоритм идентификации модели.
4) Алгоритм построения доверительного интервала для прогнозных значений.
Далее подробно рассмотрены все перечисленные выше алгоритмы.
3.1. Алгоритм экстраполяции временного ряда без учета внешних факторов
Модель экстраполяции временного ряда без учета внешних факторов сформулирована в разделе 2.1. диссертации. Алгоритм экстраполяции состоит из следующих шагов.
- Определить выборку новой истории.
- Определить выборку максимального подобия.
- Определить выборку базовой истории.
- Вычислить прогнозные значения.
Далее приведем описание каждого указанного выше шага, иллюстрируя расчеты решением следующей задачи. Пусть даны значения временного ряда цен на электроэнергию европейской территории РФ (№1 в таблице 7) с 01.09.2006 до 22.06.2009; длина временного ряда равна 24 624. Обозначим временной ряд Z(t). Требуется определить 24 значения временного ряда цен за 23.06.2009. Считаем параметр модели M = 216 заданным.
1) Определить выборку новой истории.
Выборкой новой истории является выборка временного ряда, значения которой предшествуют моменту прогноза . В текущей постановке задачи выборка новой истории равна 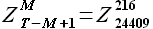 .
.
2) Определить выборку максимального подобия.
Для определения выборки максимального подобия необходимо определить значения модуля линейной корреляции 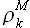 для выборки
для выборки 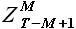 и всех выборок с задержкой k = {1,2,...,T-M-1}. При этом для каждого значения k из указанного диапазона требуется решить задачу аппроксимации выборки
и всех выборок с задержкой k = {1,2,...,T-M-1}. При этом для каждого значения k из указанного диапазона требуется решить задачу аппроксимации выборки 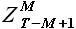 при помощи выборки
при помощи выборки 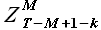 . Обозначим момент времени T-M+1 = t и решим данную задачу.
. Обозначим момент времени T-M+1 = t и решим данную задачу.
Вычислим аппроксимированные значения выборки
а с учетом обозначения
Согласно методу наименьших квадратов, коэффициенты аппроксимации определим, исходя из уравнения
где значение элементов матрицы 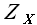 и
и 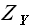 определяются следующим образом:
определяются следующим образом:
Найденные коэффициенты аппроксимации подставим в (3.1), а далее определим значение модуля корреляции 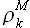 по выражению (2.22). Повторяя вычисления для каждого значения k из указанного диапазона, определим множество значений
по выражению (2.22). Повторяя вычисления для каждого значения k из указанного диапазона, определим множество значений 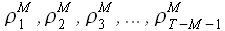 . Значения
. Значения 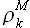 для k = {1,2,...,1000} приведены на рисунке 3.1.
для k = {1,2,...,1000} приведены на рисунке 3.1.
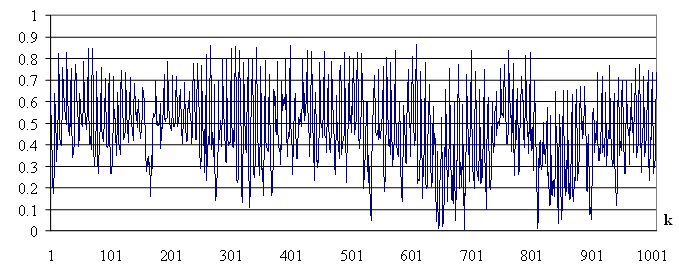
Рис. 3.1. Значения меры подобия 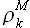 для k = {1,2,...,1000}
для k = {1,2,...,1000}
Далее на основании (2.23) определим значение максимума корреляции 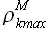 и соответствующую задержку kmax. Для решаемой задачи значение максимума корреляции
и соответствующую задержку kmax. Для решаемой задачи значение максимума корреляции 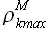 = 0.862 и соответствует задержке kmax = 9817. Для задержки уравнение аппроксимации имеет вид
= 0.862 и соответствует задержке kmax = 9817. Для задержки уравнение аппроксимации имеет вид
Результаты аппроксимации представлены на рисунке 3.2.
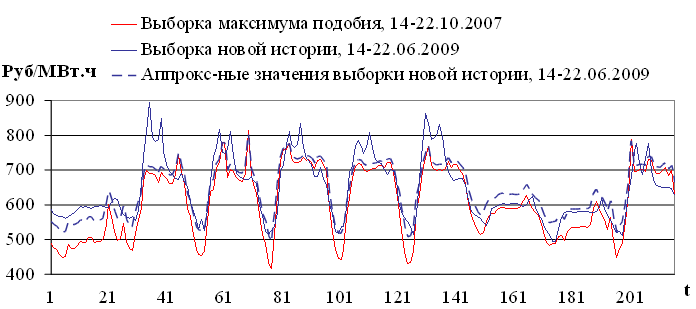
Рис. 3.2. Пример аппроксимации
3) Определить выборку базовой истории.
Согласно гипотезе подобия (2.1.3.), в качестве выборки базовой истории 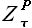 берем выборку следующую за выборкой максимального подобия
берем выборку следующую за выборкой максимального подобия 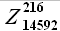 , то есть выборка базовой истории равна
, то есть выборка базовой истории равна 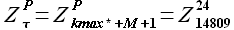 .
.
4) Вычислить прогнозные значения.
Вычислим значения выборки 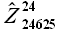 , согласно зависимости
, согласно зависимости
Результат экстраполяции представлен на рисунке 3.3.
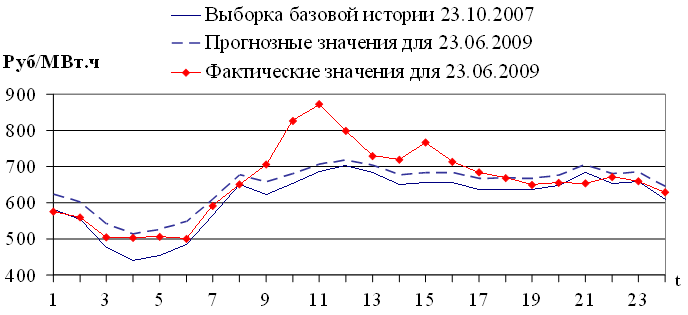
Рис. 3.3. Результат экстраполяции 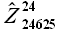 , выборка базовой истории и фактические значения цен на электроэнергию
, выборка базовой истории и фактические значения цен на электроэнергию
Значение MAPE (2.10) аппроксимации (3.5) равно 5.39%, значение MAE (2.9) равно 35.69 руб/МВт·ч. Оценки точности для модели экстраполяции (3.6): MAPE = 6.21%; MAE = 43.16 руб/МВт·ч. Результаты показывают, что ошибка аппроксимации близка, но не равна ошибке экстраполяции. Зависимость ошибок экстраполяции и аппроксимации рассмотрена в разделе 3.4.
После описания шагов алгоритма экстраполяции необходимо провести оценку времени вычислений прогнозных значений при его программной реализации.
Оценка времени расчета прогнозных значений. Разработанный алгоритм экстраполяции реализован при помощи программного комплекса MATLAB [46]. Эксперименты проводились на персональном компьютере следующей модификации:
- процессор Intel Core 2 Duo E7400 2.80 ГГц, 2ГБ DDR2
- материнская плата AsusP5KPL-CM
Оценка производительности данного персонального компьютера при помощи теста Java Micro Benchmark составляет 828 единиц. Оценки производительности компьютеров и серверов при помощи данного теста колеблются в широком диапазоне от 95 до 22 054 единиц [47].
Время расчета прогнозных значений временного ряда tp зависит от длины временного ряда T и производительности компьютера. Одной из особенностей модели экстраполяции является то, что P прогнозных значений определяются за один пробег алгоритма, например, время расчета одного значения вперед равно времени расчета 24 значений вперед. Экспериментальная зависимость времени расчета tp от длины временного ряда T для указанного персонального компьютера представлена на рисунке 3.4, значения представлены в таблице 2.
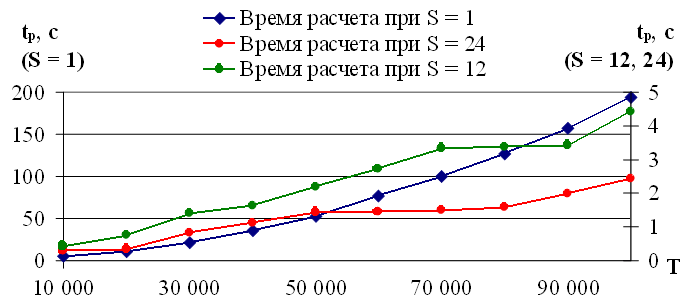
Рис. 3.4. Экспериментальная зависимость времени расчета tp от длины временного ряда T
На рисунке 3.4 приведены три зависимости времени расчета на 24 значения вперед tp от длины временного ряда T при условии, что множество значений модуля корреляции 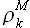 определяется с шагом
определяется с шагом
1) S = 1, т. е. вычисляются значения 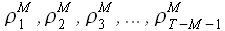 ;
;
2) S = 12, т. е. вычисляются значения 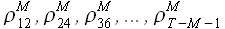 ;
;
3) S = 24, т. е. вычисляются значения 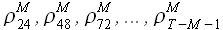 .
.
Таблица 2. Значения времени расчета при различной длине временного ряда
| Длина временного ряда T | Время расчета tp, с S = 1 |
Время расчета tp, с S = 12 |
Время расчета tp, с S = 24 |
|---|---|---|---|
| 10 000 | 5.08 | 0.43 | 0.29 |
| 20 000 | 11.12 | 0.76 | 0.33 |
| 30 000 | 21.80 | 1.41 | 0.83 |
| 40 000 | 35.73 | 1.63 | 1.11 |
| 50 000 | 52.87 | 2.19 | 1.43 |
| 60 000 | 77.17 | 2.72 | 1.45 |
| 70 000 | 99.61 | 3.32 | 1.49 |
| 80 000 | 126.68 | 3.38 | 1.59 |
| 90 000 | 156.85 | 3.42 | 1.99 |
| 100 000 | 193.90 | 4.42 | 2.44 |
Шаг S = 24 применяется для прогнозирования энергопотребления, цен энергорынка РФ (4.1). Шаг перебора значений модуля корреляции 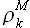 определяется экспертом и может варьироваться в зависимости от сезонности временного ряда.
определяется экспертом и может варьироваться в зависимости от сезонности временного ряда.
Согласно оценке [48], высокой считается скорость, при которой вычисление 24 прогнозных значений занимает не более 20 минут. Время расчета 24 значений временного ряда длинной 100 000 значений и переборе значений 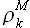 с шагом S = 1 составляет около 200 секунд на указанном персональном компьютере. При шаге S = 12 аналогичное время расчетов не превышает 5 секунд; при S = 24 — 2.5 секунд (таблица 2). Данные оценки подтверждают высокую скорость вычислений предложенного алгоритма экстраполяции временного ряда без учета внешних факторов.
с шагом S = 1 составляет около 200 секунд на указанном персональном компьютере. При шаге S = 12 аналогичное время расчетов не превышает 5 секунд; при S = 24 — 2.5 секунд (таблица 2). Данные оценки подтверждают высокую скорость вычислений предложенного алгоритма экстраполяции временного ряда без учета внешних факторов.
3.2. Алгоритм экстраполяции временного ряда с учетом внешних факторов
Модель экстраполяции временного ряда с учетом внешних факторов сформулирована в разделе 2.2 диссертации. Алгоритм экстраполяции состоит из следующих шагов.
- Определить выборку новой истории.
- Определить выборку максимального подобия.
- Определить выборку базовой истории.
- Вычислить прогнозные значения.
Далее приведем описание каждого указанного шага, иллюстрируя расчеты решением следующей задачи. Пусть даны значения временного ряда цен на электроэнергию европейской территории РФ (№1 в таблице 7) с 01.09.2006 до 22.06.2009; а также значения временного ряда энергопотребление европейской территории РФ (№1 в таблице 11) с 01.09.2006 до 22.06.2009. Обозначим временной ряд цен на электроэнергию Z(t), временной ряд энергопотребления – X(t). Требуется определить 24 значения временного ряда за 23.06.2009 с учетом влияния временного ряда энергопотребления X(t). Считаем параметр модели M = 216 заданным.
В связи с тем, что значения временного ряда X(t) доступны до той же отметки времени, что и значения временного ряда Z(t), необходимо на первом этапе определить значения временного ряда 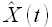 в сутках 23.06.2009 по алгоритму, рассмотренному подробно в разделе 3.1. На втором этапе полученные экстраполированные значения
в сутках 23.06.2009 по алгоритму, рассмотренному подробно в разделе 3.1. На втором этапе полученные экстраполированные значения 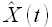 использовать при вычислении экстраполированных значений
использовать при вычислении экстраполированных значений 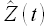 .
.
Алгоритм расчета  рассмотрен в предыдущем разделе. Модель экстраполяции временного ряда X(t) имеет вид
рассмотрен в предыдущем разделе. Модель экстраполяции временного ряда X(t) имеет вид
и оценку точности: MAPE = 1.07%; MAE = 782 МВт·ч. Считаем задачу определения 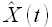 решенной.
решенной.
1) Определить выборку новой истории.
Выборкой новой истории временного ряда Z(t) является выборка временного ряда, значения которой предшествуют моменту прогноза T. В текущей постановке задачи выборка новой истории равна 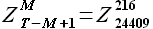 . Выборка новой истории соответствует значениям цены на электроэнергию за период с 14.06.2009 до 22.06.2009.
. Выборка новой истории соответствует значениям цены на электроэнергию за период с 14.06.2009 до 22.06.2009.
2) Определить выборку максимального подобия.
Для определения выборки максимального подобия необходимо определить значения ошибки регрессии  (2.29) для выборки
(2.29) для выборки 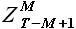 и всех выборок с задержкой k = {1,2,...,T-M-1}. При этом для каждого значения k из указанного диапазона требуется решить задачу аппроксимации выборки
и всех выборок с задержкой k = {1,2,...,T-M-1}. При этом для каждого значения k из указанного диапазона требуется решить задачу аппроксимации выборки 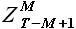 при помощи выборок
при помощи выборок 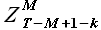 и
и 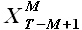 . Обозначим момент времени T-M+1 = t и решим данную задачу.
. Обозначим момент времени T-M+1 = t и решим данную задачу.
Вычислим аппроксимированные значения выборки
а с учетом обозначения
Согласно методу наименьших квадратов, коэффициенты аппроксимации определим исходя из уравнения
где матрицы 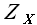 и
и 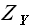 определяются следующим образом:
определяются следующим образом:
Например, для задержки k = 11689 коэффициенты аппроксимации равны
Найденные коэффициенты аппроксимации подставим в выражение (3.8), а далее определим значение ошибки регрессии 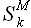 (2.29). Повторяя вычисления для каждого значения k из указанного диапазона, определим множество значений
(2.29). Повторяя вычисления для каждого значения k из указанного диапазона, определим множество значений 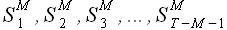 .
.
Далее на основании (2.21) определим значение минимума ошибки регрессии 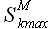 и соответствующую задержку kmax. Для решаемой задачи минимальная ошибка
и соответствующую задержку kmax. Для решаемой задачи минимальная ошибка 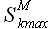 = 137337.65 соответствует задержке kmax = 11689. Для задержки kmax уравнение аппроксимации имеет вид
= 137337.65 соответствует задержке kmax = 11689. Для задержки kmax уравнение аппроксимации имеет вид
Выборка 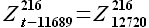 соответствует значениям временного ряда за период с 05.06.2008 по 13.06.2008. Результаты аппроксимации представлены на рисунке 3.5.
соответствует значениям временного ряда за период с 05.06.2008 по 13.06.2008. Результаты аппроксимации представлены на рисунке 3.5.
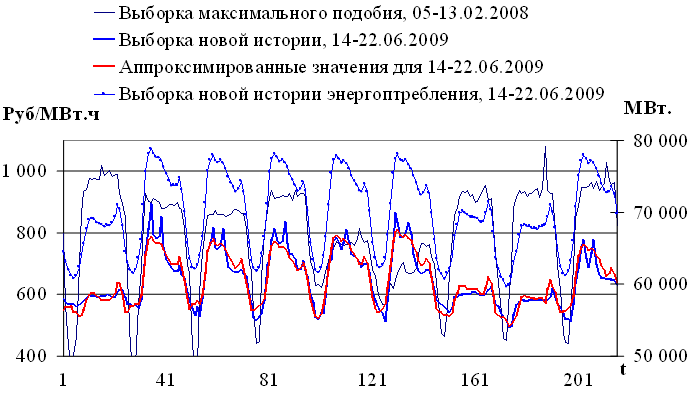
Рис. 3.5. Пример аппроксимации с учетом внешнего фактора
3) Определить выборку базовой истории.
Согласно гипотезе подобия (2.2.3.), в качестве выборки базовой истории 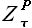 берем выборку, следующую за выборкой максимального подобия
берем выборку, следующую за выборкой максимального подобия 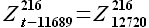 , то есть выборка базовой истории равна
, то есть выборка базовой истории равна 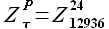 .
.
4) Вычислить прогнозные значения.
Вычислим значения выборки 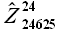 согласно зависимости
согласно зависимости
Результат экстраполяции представлен на рисунке 3.6.
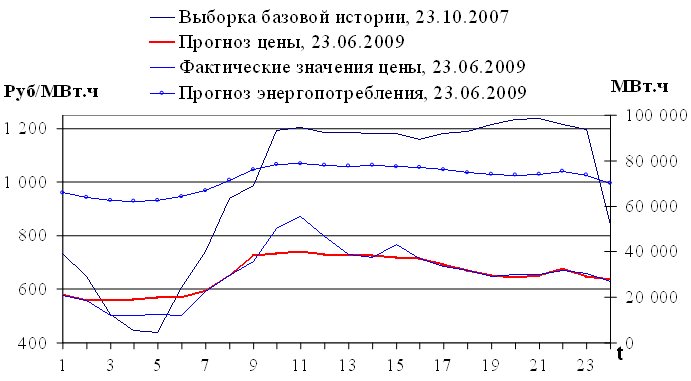
Рис. 3.6. Результат экстраполяции цен на электроэнергию с учетом энергопотребления
Оценки ошибки аппроксимации: значение MAPE аппроксимации (3.8) равно 2.11%, значение MAE = 12.24 руб/МВт·ч. Оценки точности для модели экстраполяции (3.14): MAPE = 4.42%; MAE = 28.29 руб/МВт·ч. Результаты показывают, что ошибка аппроксимации близка, но не равна ошибке экстраполяции. Зависимость ошибок экстраполяции и аппроксимации рассмотрена в разделе 3.4.
На основании сравнения результатов расчета прогнозных значений цен на электроэнергию в предыдущем и текущих разделах диссертации, т. е. без учета и с учетом одного внешнего фактора, утверждаем, что учет внешнего фактора может приводить к повышению точности прогнозирования, как это получилось в рассмотренной задаче. Подробнее данная особенность модели рассмотрена в разделе 4.1.2.
После описания алгоритма экстраполяции необходимо произвести оценку времени вычисления прогнозных значения при программной реализации данного алгоритма.
Оценка времени расчета прогнозных значений. Разработанный алгоритм экстраполяции временного ряда с учетом внешних факторов реализован при помощи программного комплекса MATLAB. Эксперименты проводились на указанном в предыдущем разделе персональном компьютере.
Время расчета tp будущий значений временного ряда зависит от длины временного ряда T, количества внешних факторов и производительности компьютера. Для модели с учетом внешних факторов время tp не зависит от времени упреждения P.
Зависимость времени расчета tp от длины временного ряда T при экстраполяции с учетом одного внешнего фактора с использованием указанного персонального компьютера представлена на рисунке 3.7, значения представлены в таблице 3.
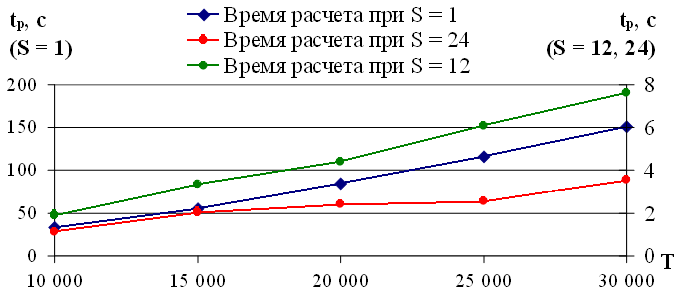
Рис. 3.7. Зависимость времени расчета tp от длины временного ряда T при экстраполяции с учетом одного внешнего фактора
Таблица 3. Значения времени расчета при различной длине временного ряда для экстраполяции с учетом одного внешнего фактора
| Длина временного ряда T | Время расчета tp, с S = 1 |
Время расчета tp, с S = 12 |
Время расчета tp, с S = 24 |
|---|---|---|---|
| 10 000 | 33.28 | 1.91 | 1.14 |
| 15 000 | 55.29 | 3.32 | 2.04 |
| 20 000 | 84.41 | 4.40 | 2.43 |
| 25 000 | 115.40 | 6.06 | 2.57 |
| 30 000 | 150.95 | 7.62 | 3.53 |
На рисунке 3.7 приведены три зависимости времени расчета 24 значений вперед tp на модели с учетом одного внешнего фактора от длины временного ряда T при условии, что множество значений 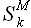 определяется с шагом S = 1, S = 12, S = 24 (раздел 3.1.). Полученные оценки значений tp находятся в диапазоне от 33 до 150 секунд для S = 1; для S = 12, S = 24 величина tp не превышает 8 секунд при длине временного ряда 30 000 значений (таблица 3). На основании полученных оценок tp сделаем вывод о высокой скорости вычислений экстраполированных значений временного ряда с учетом одного внешнего фактора [48].
определяется с шагом S = 1, S = 12, S = 24 (раздел 3.1.). Полученные оценки значений tp находятся в диапазоне от 33 до 150 секунд для S = 1; для S = 12, S = 24 величина tp не превышает 8 секунд при длине временного ряда 30 000 значений (таблица 3). На основании полученных оценок tp сделаем вывод о высокой скорости вычислений экстраполированных значений временного ряда с учетом одного внешнего фактора [48].
Рассмотрим зависимость расчета tp от длины временного ряда T при экстраполяции с учетом двух внешних факторов при вычислениях на указанном персональном компьютере (рис. 3.8).
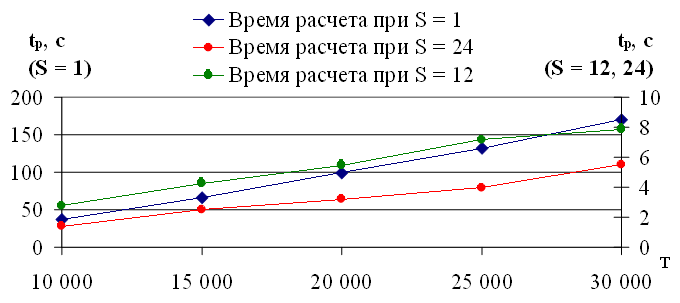
Рис. 3.8. Зависимость времени расчета tp от длины временного ряда T при экстраполяции с учетом двух внешних факторов
Таблица 4. Значения времени расчета при различной длине временного ряда для экстраполяции с учетом двух внешних факторов
| Длина временного ряда T | Время расчета tp, с S = 1 |
Время расчета tp, с S = 12 |
Время расчета tp, с S = 24 |
|---|---|---|---|
| 10 000 | 37.44 | 2.77 | 1.39 |
| 15 000 | 65.86 | 4.26 | 2.52 |
| 20 000 | 98.51 | 5.47 | 3.21 |
| 25 000 | 131.97 | 7.13 | 3.95 |
| 30 000 | 170.39 | 7.87 | 5.48 |
На рисунке 3.8 приведены три зависимости времени расчета 24 значений вперед tp на модели экстраполяции с учетом двух внешних факторов от длины временного ряда T при условии, что множество значений 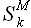 определяется с шагом S = 1, S = 12, S = 24 (раздел 3.1.). Полученные оценки значений tp находятся в диапазоне от 37 до 170 секунд для S = 1; для S = 12, S = 24 величина tp не превышает 8 секунд.
определяется с шагом S = 1, S = 12, S = 24 (раздел 3.1.). Полученные оценки значений tp находятся в диапазоне от 37 до 170 секунд для S = 1; для S = 12, S = 24 величина tp не превышает 8 секунд.
Отметим, что при увеличении числа внешних факторов с одного до двух время расчета tp для аналогичных значений T существенно не изменилось. Например, при T = 30 000 и S = 1 при одном внешнем факторе значение tp = 151 секунда; при двух внешних факторах аналогичное значение — tp = 170 секунд. Таким образом, разница составила менее 20 секунд.
На основании полученных оценок значений tp заключим высокую скорость вычисления будущих значений предложенного алгоритма экстраполяции временного ряда с учетом внешних факторов [48].
3.3. Алгоритм идентификации модели
3.3.1. Описание алгоритма
В настоящем разделе предложен алгоритм идентификации моделей EMMSP (2.25) и EMMSPX (2.34). Задача идентификации состоит в нахождении параметра модели M, который определяет длину выборок новой истории и максимального подобия (рис. 2.6, 2.7). Выполним идентификацию обеих моделей по одному алгоритму.
1) Определить тестовый и контрольный периоды временного ряда.
2) Определить время упреждения P и диапазон возможных значений параметра M.
3) Прогнозировать тестовый период на P значений вперед при всех значениях параметра M из установленного диапазона.
5) Построить зависимость ошибки прогнозирования от M.
6) Экспертно определить окончательное значение параметра M.
Рассмотрим указанные шаги идентификации подробнее.
1) Определить тестовый и контрольный периоды временного ряда.
На данном шаге исходный временной ряд Z(t) разделим на три части в пропорции, например, 1:1:1. Полученные части назовем базовый период (33%), тестовый период (33%) и контрольный период (34%) временного ряда, соответственно, как показано на рисунке 3.9.
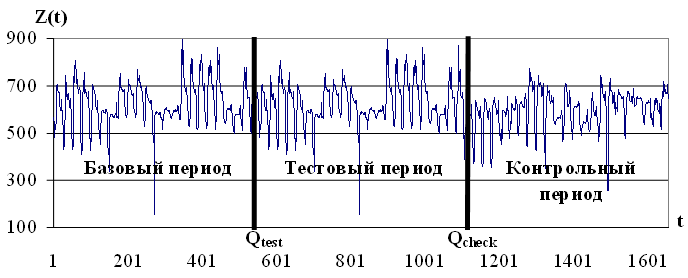
Рис. 3.9. Разделение временного ряда на периоды
2) Определить время упреждения P и диапазон возможных значений параметра M.
Далее, исходя из решаемой задачи прогнозирования временного ряда, требуется определить время упреждения P, а также диапазон возможных значений параметра M. Первоначально рекомендуем брать широкий диапазон возможных значений M, например, M = {2P,...,15P}. Значения M можно перебирать с шагом S = 1, т. е. M = {P+1,P+2,...,15P}. Однако практика решения данной задачи показала, что удобнее перебирать значения параметра M с шагом S = P или S = 0.5P, т. е. M = {P,1.5P,2P,...,15P}. Данный подход сокращает время идентификации, существенно не влияя на точность последующего прогнозирования.
3) Прогнозировать тестовый период на P значений вперед при всех значениях параметра M из установленного диапазона.
Для каждого значения параметра M из установленного диапазона, прогнозируем значения временного ряда на P значений вперед внутри тестового периода. Рекомендуем устанавливать длину тестового периода в диапазоне от 150P до 300P.
По результатам прогнозирования для каждого значения M определяем среднюю абсолютную ошибку прогноза для всего тестового периода
где K – количество значений временного ряда, попавших внутрь тестового периода, Qtest(t) – начало тестового периода на оси времени (рис. 3.9),  – прогнозные значения, полученные при прогнозировании с параметром модели M.
– прогнозные значения, полученные при прогнозировании с параметром модели M.
4) Построить зависимость ошибки прогнозирования от M.
Строим график зависимости MAE(M) для тестового периода и определяем диапазон значений M, соответствующий устойчивому минимуму MAE(M).
Рассмотрим в качестве примера зависимость MAE(M) для временного ряда энергопотребления европейской территории РФ, представленного на рисунке 3.10. Первоначально был выбран диапазон M = {36,48,...,360}, внутри которого выделен диапазон устойчивого минимума ошибки M = {168,180,...,240}.
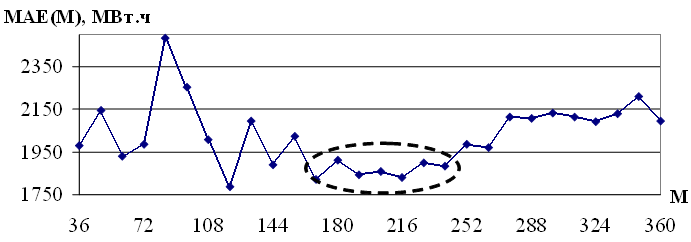
Рис. 3.10. Зависимость MAE(M) для M = {36,48,...,360}
На рисунке 3.10 представлен типичный вид зависимости MAE(M), при малых и больших значениях M из диапазона M = {P,1.5P,2P,...,15P} ошибка, как правило, велика. Однако существует стабильный минимум значений MAE(M) для некоторых промежуточных значений M. В приведенном примере значения параметра M перебирались с шагом S = 0.5P.
5) Экспертно определить значение параметра M.
На последнем шаге экспертом выбирается значение параметра модели M внутри диапазона устойчивого минимума.
Рекомендуем выбирать значение M таким образом, чтобы значения MAE(M) для соседних точек примерно совпадали со значением M для выбранного значения M. В случае, если устойчивый минимум значений MAE(M) лежит близко к левой границе исследуемого диапазона M, то рекомендуем брать наибольшее значение из диапазона устойчивого минимума.
После выполнения всех шагов алгоритма задача идентификации решена и модель может применяться для прогнозирования контрольного периода.
3.3.2. Распараллеливание вычислений
Наиболее ресурсоемкий шаг в смысле времени и вычислительных мощностей в предложенном алгоритме идентификации модели состоит в прогнозировании тестового периода при различных значениях параметра модели M из установленного диапазона (шаг 3). В связи с тем, что результаты прогнозирования при одном значении параметра M не зависят от результатов прогнозирования при другом значении M, данный процесс может быть распараллелен следующим образом.
1) Разделить тестовый период временного ряда на непересекающиеся подпериоды, объединение которых дает тестовый период.
2) Производить параллельно вычисления прогнозных значений для подпериодов при различных значениях параметра M.
В таблице 5 проиллюстрирована схема распараллеливания вычислений.
Таблица 5. Схема распараллеливания вычисления при идентификации
| Значение параметра M | Тестовый подпериод №1 | Тестовый подпериод №2 | ... | Значение MAE(M) |
|---|---|---|---|---|
| M1 | MAE№1(M1) | MAE№2(M1) | ... | MAE(M1) |
| M2 | MAE№1(M2) | MAE№2(M2) | ... | MAE(M2) |
| M3 | MAE№1(M3) | MAE№2(M3) | ... | MAE(M3) |
| ... | ... | ... | ... | ... |
Для значения параметра модели M1 производится прогноз внутри тестового подпериода №1 и определяется величина ошибки MAE№1(M1). Параллельно с данными вычислениями производятся оценки остальных величин MAE№q(Mi). После завершения всех вычислений итоговые значения MAE(M1) определяются как средние величины от множества значений оценок ошибки MAE№1(M1), MAE№2(M1),...,MAE№q(M1) соответствующих рассматриваемому значению параметра M1.
В случае ужесточения требований по скорости идентификации модели количество тестовых подпериодов должно быть увеличено.
3.3.3. Наборы моделей
Решением задачи идентификации модели экстраполяции является значение параметра M. В случае если сформированная модель EMMSP(M) или EMMSPX(M) имеет недостаточную точность прогнозирования, возможно повышение точности за счет использования различных моделей для различных отрезков временного ряда.
Пусть необходимо прогнозировать временной ряд Z(t). При этом искомый временной ряд Z(t) можно очевидным образом разбить на некоторые чередующие отрезки, например, временной ряд, имеющий почасовое разрешение, может быть разбит по дням недели, месяцам и т. д. Тогда в процессе идентификации модели необходимо определять параметр модели M для каждого установленного отрезка отдельно. Иллюстрацией такого набора моделей для прогнозирования временного ряда, имеющего почасовое разрешение, является таблица 6.
Таблица 6. Набор моделей для прогнозирования временного ряда, имеющего почасовое разрешение
| День недели | Параметр модели |
|---|---|
| Понедельник | M1 |
| Вторник | M2 |
| Среда | M3 |
| Четверг | M4 |
| Пятница | M5 |
| Суббота | M6 |
| Воскресенье | M7 |
В данном примере каждому дню недели соответствует собственное значение параметра M: при прогнозе значений понедельника используется модель EMMSP(M1), при прогнозе вторника — EMMSP(M2) и т. д.
Получить набор моделей для временного ряда можно на основании результатов идентификации модели следующим образом.
1) Разбить результаты прогнозирования тестового периода при различных значениях параметра M в соответствии с установленными заранее отрезками временного ряда (например, по дням недели).
2) Определить зависимость MAE(M) для каждого отрезка.
3) Определить диапазон устойчивого минимума и окончательное значение параметра M для каждого отрезка отдельно.
Наборы моделей применялись для прогнозирования временных рядов энергорынка РФ. Результаты прогнозирования цен на электроэнергию и энергопотребление, представленные в разделах 4.1.2. и 4.1.3. диссертации, подтверждают, что применение наборов повышает точность прогнозирования (таблицы 10 и 14).
3.3.4. Оценка времени идентификации
Идентификация модели, предложенная в настоящем разделе диссертации, имеет следующую оценку времени вычислений на шаге №3 (остальные шаги не требуют оценки времени)
Здесь tid – время идентификации в секундах, TTEST – длина тестового периода временного ряда, P – время упреждения, NM – количество возможных значений параметра, PC – оценка производительности компьютера по тесту Java Micro Benchmark [47]. Время расчета tp определяется по таблицам 2, 3 и 4. В случае если длина временного ряда превышает диапазоны, заданные в таблицах, то необходимо линейно экстраполировать значения tp при соответствующем шаге перебора значений задержки k при определении множества значений модуля корреляции.
Для иллюстрации приведенной оценки рассмотрим пример идентификации временного ряда энергопотребления европейской территории РФ (№1 в таблице 11). Временной ряд содержит значения за период с 01.09.2006 по 07.08.2011, длина временного ряда T = 43224 значения. В качестве тестового периода выбираем с 07.08.2009 по 06.08.2010, в качестве контрольного периода выбираем период с 07.08.2010 по 07.08.2011. При этом длина тестового и контрольного периодов равна 8 760 значений.
Для рассматриваемого примера TTEST = 8760; в связи с тем, что идентификации выполнялась на указанном персональном компьютере, оценка его производительности PC = 828. Время упреждения P = 24, количество значений параметра M в оцениваемом диапазоне NM = 28 (рис. 3.10). Начало тестового периода определяется QTEST = 25704, таким образом прогнозирование временного ряда производится в диапазоне {24704,..,24464}. Перебор значений задержки производится с шагом S = 12. Обратившись к таблице 2, находим оценку значения tp = 1.63 и получаем
Таким образом, для идентификации временного ряда энергопотребления европейской территории РФ необходимо 4.63 часа работы указанного в разделе 3.1. типа персонального компьютера.
В случае если произведенная оценка времени идентификации слишком высока, то существенное сокращение времени может быть достигнуто применением параллельных вычислений (раздел 3.3.2.).
3.4. Алгоритм построения доверительного интервала
В настоящем разделе рассмотрен алгоритм построения доверительного интервала прогнозных значений для разработанной модели экстраполяции.
Выборки максимального подобия  и новой истории
и новой истории 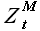 связаны соотношением
связаны соотношением
а выборки прогноза 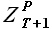 и базовой истории
и базовой истории 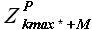 – соотношением
– соотношением
Исследования векторов ошибок аппроксимации Eapp и экстраполяции Eext показали, что
- распределения значений ошибок Eapp и Eext не являются нормальными (проверялось по критерию Пирсона при уровне значимости pValue = 0.05),
- распределение значений ошибок аппроксимации Eapp не согласуется с распределением значений ошибок экстраполяции Eext (проверялось по критерию Колмогорова-Смирнова при уровне значимости pValue = 0.05),
- среднее значение обеих ошибок близко к нулю,
- дисперсия ошибки аппроксимации Eapp отлична от дисперсии ошибки экстраполяции Eext,
- асимметрия обеих ошибок отлична от нуля, колеблется в диапазоне от 0.5 до 1.8 для исследуемых временных рядов,
- эксцесс обеих ошибок больше единицы, колеблется в диапазоне от 3 до 15 для исследуемых временных рядов.
На рисунке 3.11 представлены гистограммы выборок Eapp и Eext для временного ряда цен на электроэнергию европейской территории РФ.
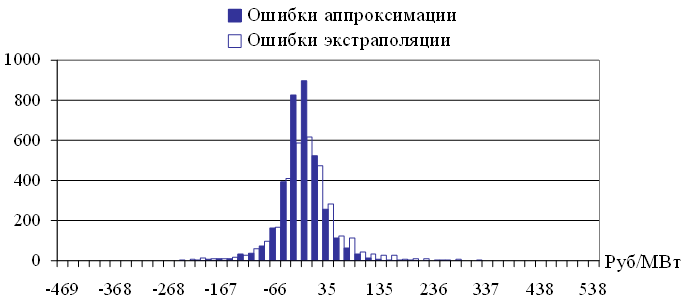
Рис. 3.11. Гистограммы выборок Eapp и Eext
Постановка задачи. В процессе прогнозирования значений временного ряда Z(t) вычисляем вектор ошибок аппроксимации 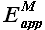 (2.1.2. и 2.2.2.). Требуется определить асимметричный доверительный интервал для прогнозных значений
(2.1.2. и 2.2.2.). Требуется определить асимметричный доверительный интервал для прогнозных значений  для заданной вероятности p, используя значения ошибок аппроксимации
для заданной вероятности p, используя значения ошибок аппроксимации 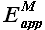
Здесь значения 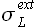 и
и 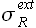 соответствуют левому (индекс L) и правому (индекс R) доверительному интервалу. Обозначим значение вероятности малой буквой p, чтобы не путать с временем упреждения P.
соответствуют левому (индекс L) и правому (индекс R) доверительному интервалу. Обозначим значение вероятности малой буквой p, чтобы не путать с временем упреждения P.
Решение задачи. Построим гистограмму значений Eapp. Пример гистограммы приведен на рисунке 3.12.
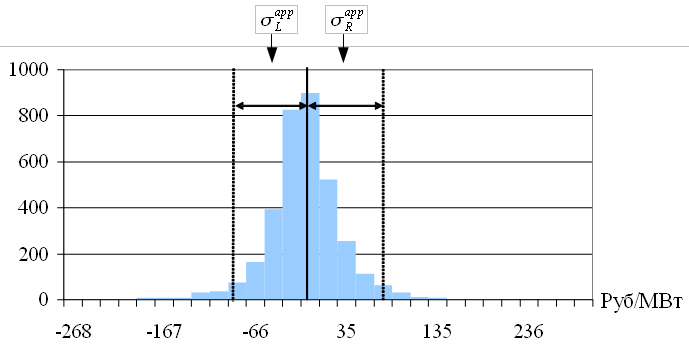
Рис. 3.12. Гистограмма выборки Eapp
Полную площадь гистограммы можно определить как сумму левой и правой половин относительно среднего значения ошибки
Для заданной вероятности p площадь гистограммы ограниченна 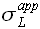 и
и 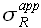 , а потому
, а потому
Определим значение левой границы доверительного интервала 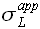 таким образом, чтобы площадь, ограниченная
таким образом, чтобы площадь, ограниченная 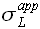 и средним значением, была равна p * SL. Аналогичным образом определим правую границу доверительного интервала
и средним значением, была равна p * SL. Аналогичным образом определим правую границу доверительного интервала 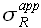 . Используя тот же подход, определим значения границ доверительных интервалов
. Используя тот же подход, определим значения границ доверительных интервалов 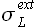 ,
, 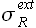 для вектора ошибок экстраполяции Eapp.
для вектора ошибок экстраполяции Eapp.
Исследование границ доверительных интервалов ошибок аппроксимации 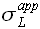 ,
, 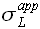 и экстраполяции
и экстраполяции 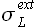 ,
, 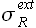 показали, что значения
показали, что значения 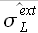 ,
, 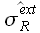 могут быть с высокой точностью определены при помощи линейных зависимостей
могут быть с высокой точностью определены при помощи линейных зависимостей
где 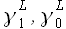 и
и 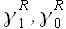 – коэффициенты.
– коэффициенты.
При прогнозировании тестового периода определим фактические значения ошибок аппроксимации Eapp и экстраполяции Eext для результирующего значения параметра модели M. На основании данных векторов для всех вероятностей p = [0;1] с шагом 0.01 определим пары значений 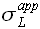 ,
,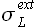 и
и 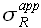 ,
,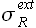 . Далее при помощи метода наименьших квадратов вычислим значения коэффициентов и , соответственно.
. Далее при помощи метода наименьших квадратов вычислим значения коэффициентов и , соответственно.
На рисунке 3.13 представлены фактические и модельные значения доверительных интервалов для вероятностей p = {0.50,0.51,...,1} для временного ряда цен на электроэнергию европейской территории РФ.
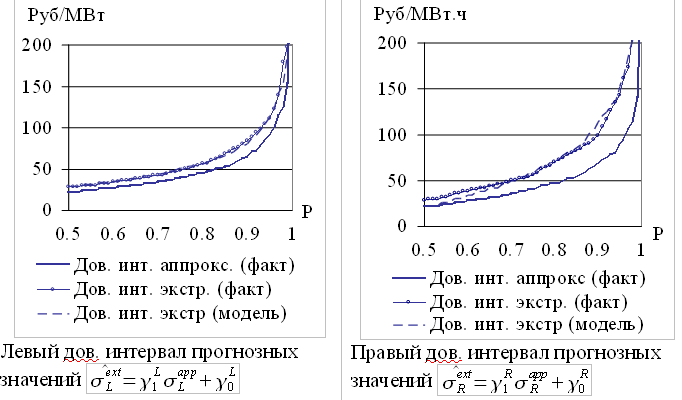
Рис. 3.13. Моделирование доверительных интервалов
Среднее отклонение в процентах (2.10) рассчитанных значений 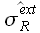 от фактических
от фактических 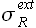 и отклонений
и отклонений 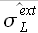 от
от 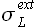 границ доверительного интервала для исследованных временных рядов колеблется в диапазоне от 1% до 8%. Полученная точность моделирования границ доверительного интервала достаточна для работы с исследуемыми временными рядами.
границ доверительного интервала для исследованных временных рядов колеблется в диапазоне от 1% до 8%. Полученная точность моделирования границ доверительного интервала достаточна для работы с исследуемыми временными рядами.
Алгоритм построения доверительного интервала для прогнозных значений состоит из двух частей – определение модели границ доверительного интервала (3.23) и вычисление границ для новых прогнозных значений.
Для определения моделей границ доверительного интервала (3.23) необходимо выполнить следующие шаги.
1) Произвести прогнозирование тестового периода и оценить ошибки аппроксимации Eapp и экстраполяции Eext, соответствующие окончательному значению параметра M.
2) На основании векторов ошибок для всех вероятностей p = {0.50,0.51,...,1} определить пары значений границ доверительных интервалов 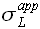 ,
,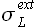 и
и 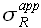 ,
,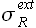 как описано выше.
как описано выше.
3) При помощи метода наименьших квадратов вычислить коэффициенты зависимости (3.23).
Модели границ доверительного интервала также как и параметр модели M определяются в процессе идентификации модели экстраполяции. Для вычисления границ доверительного интервала новых прогнозных значений необходимо выполнить следующие шаги.
1) Произвести прогнозирование временного ряда и получить вектор ошибок аппроксимации 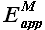 .
.
2) На основании полученного вектора 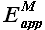 определить значения границ доверительного интервала
определить значения границ доверительного интервала 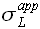 ,
, 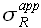 .
.
3) На основании зависимости (3.23), вычислить границы доверительного интервала для экстраполированных значений 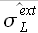 и
и 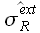 .
.
После того, как определены доверительные интервалы прогнозных значений, задача прогнозирования временного ряда считается решенной (раздел 1.2.).
3.5. Выводы
1) Разработан метод прогнозирования на базе модели экстраполяции по выборке максимального подобия.
2) Разработаны алгоритмы экстраполяции временного ряда с учетом и без учета внешних факторов. Исследования показали высокую скорость вычислений прогнозных значений.
3) Предложен алгоритм идентификации параметра модели . Алгоритм идентификации содержит вычисления, которые могут выполняться параллельно по предложенной схеме.
4) Произведена оценка времени последовательных вычислений для решения задачи идентификации модели.
5) Разработан алгоритм построения доверительного интервала для прогнозных значений.
Глава 1. Постановка задачи и обзор моделей прогнозирования временных рядов
Глава 2. Модели экстраполяции временных рядов по выборке максимального подобия
Глава 3. Метод прогнозирования на модели экстраполяции по выборке максимального подобия
Глава 4. Программная реализация и оценка эффективности модели экстраполяции по выборке максимального подобия
Список литературы
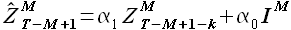 (3.1)
(3.1)
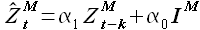 (3.2)
(3.2)
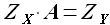 (3.3)
(3.3)
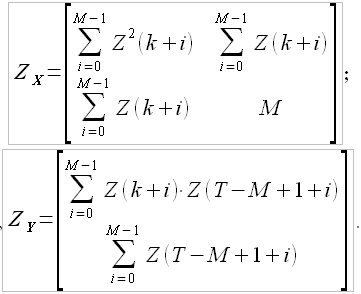 (3.4)
(3.4)
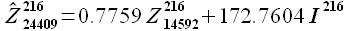 (3.5)
(3.5)
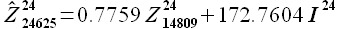 (3.6)
(3.6)
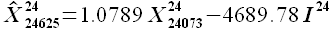 (3.7)
(3.7)
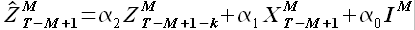 (3.8)
(3.8)
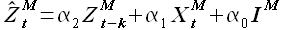 (3.9)
(3.9)
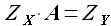 (3.10)
(3.10)
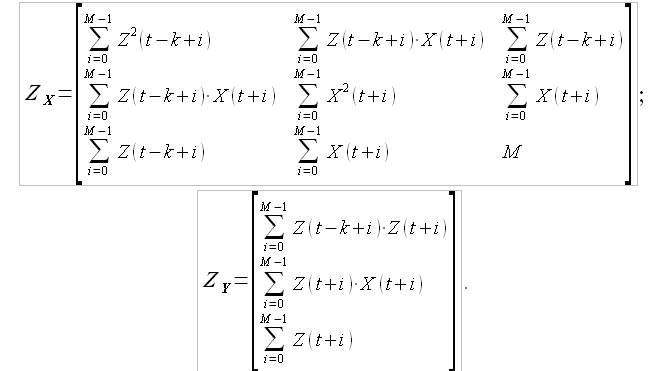 (3.11)
(3.11)
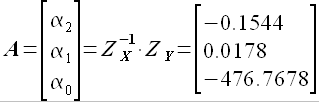 (3.12)
(3.12)
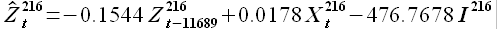 (3.13)
(3.13)
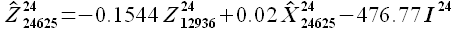 (3.14)
(3.14)
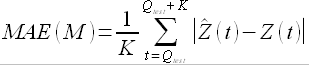 (3.15)
(3.15)
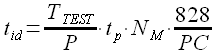 (3.16)
(3.16)
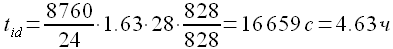 (3.17)
(3.17)
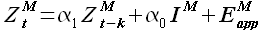 (3.18)
(3.18)
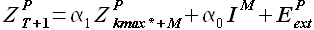 (3.19)
(3.19)
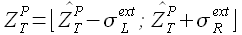 (3.20)
(3.20)
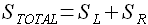 (3.21)
(3.21)
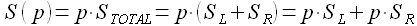 (3.22)
(3.22)
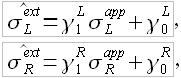 (3.23)
(3.23)
Еще один вопрос:
Формула (3.1) - i с индексом M, как я понимаю - единичный вектор? Если M = 216, то значение i = 216?
В формуле 3.1 величина I — действительно единичный вектор размера [1xM]. И этот единичный вектор умножается на α0. Таким образом, значение α0*IM = [α0, α0, ..., α0] — вектор длины M.
Пытаюсь рассмотреть Вашу модель на конкретном примере. И остановился на формуле 2.22. (При определении значения модуля корреляции).
В числителе под Суммой, где находится Z^, идет разность Z^ с Z_. Что подразумевается под этими элементами? Z^ - это вектор значений, что мы подсчитали в формуле 3.1? а Z_ - это среднее значение выборки длины M?
Мне тяжело объяснить,что конкретно вызвало затруднее, но надеюсь Вы меня поняли) Заранее спасибо!
Очень приятно, что моей моделью интересуются!
Смотрите, все очень просто: здесь нужно просто рассчитать величину корреляции. Обычно имеются встроенные функции для этого: corr(X,Y) — величина корреляции.
В коде можно условно написать так.
SourceTimeSeries — исходный временной ряд длины N;
P — время упреждения;
M — параметр модели;
q — момент прогноза;
Цикл поиска выборки максимального подобия
NewHistory = ПолучитьВыборку(SourceTimeSeries, q, M);
FOR k = 1 : N – M – 1
TemproraryOldHistory = ПолучитьВыборку(SourceTimeSeries,q – M – k, M);
Likeness(k) = abs(corr(TemproraryOldHistory, NewHistory));
END
В итоге массив Likeness(k) будет содержать в себе все значения подобия (модуля корреляции), оттуда нужно будет выбрать максимальное значение и найти TemproraryOldHistory, которая этому максимуму соответствует.
Описание функций
ПолучитьВыборку(TimeSeries, q, M) – возвращает выборку временного ряда TimeSeries с моментом начала q длины M.
abs(corr((Set1, Set2)) – возвращает значение модуля линейной корреляции для выборок Set1, Set2 согласно формуле (2.22).
Доброго времени суток, сильно заинтересовался вашей моделью, пишу диплом на основе вашей модели.
возник вопрос, мне не дает ясности формула 3.4 а именно как считаются элементы матрицы Zx.
то есть, к примеру, в ряду будет 1000 элементов и будем считать элемент (1,1) в матрице Zx, возьмем k =600.
как я понимаю ряд с задержкой будет содержать первые 400 значений исходного ряда, а в расчет будут идти последние 400 эначений ряда....получается мы ищем подобие в противоположной стороне исходной выборки?
можете разъяснить формулу?
Андрей, добрый день! Спасибо за интерес к моей работе.
Ваш вопрос стал очередным в этой серии. Для пояснения алгоритма расчета я сделала пример реализации в MATLAB. Его можно скачать в записи блога Модель прогнозирования по выборке максимального подобия: пример реализации в MATLAB. Надеюсь, что этот материал поможет разобраться.
большое спасибо вам за отзывчивость!)) буду разбиратся))