Экспоненциальное сглаживание для прогноза продаж
Ранее я подробно рассмотрела постановку задачи долгосрочного прогнозирования продаж, а также коснулась модели экспоненциального сглаживания. Теперь же я представляю результаты прогноза продаж, которых удалось добиться.
Для определения модели экспоненциального сглаживания для каждого временного ряда я расширила исходную модель следующим образом
1) Беру классическое экспоненциальное сглаживание
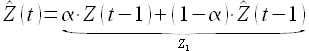
2) Обозначаю выражение Z1. Далее делаю взвешивание по Z1 следующим образом:
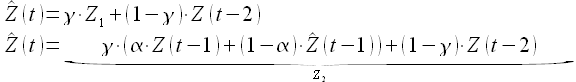
3) Обозначаю полученное выражение Z2. Далее делаю взвешивание по Z2 аналогично.
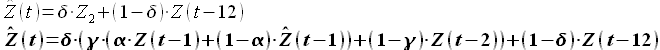
Получается немного громоздкая, но понятная формула, где ясны ограничения на значения коэффициентов: 0 ≤ α ≤ 1, 0 ≤ γ ≤ 1, 0 ≤ δ ≤ 1.
Выделенное жирным шрифтом выражение и есть модель долгосрочного прогнозирования продаж. Надо отметить, что с помощью данной модели мы прогнозируем только на один месяц вперед. При прогнозе на несколько месяцев мы используем ту же самую модель, однако считаем полученные ранее прогнозные значения фактическими.
Далее требуется найти значения коэффициентов для каждого из пяти исследуемых временных рядов. Процесс определения значений коэффициентов для конкретного временного ряда называется идентификацией модели.
Определение коэффициентов модели прогнозирования
Коэффициенты модели прогнозирования определялись простым перебором, а именно: в цикле перебирались значения от 0 до 1 с шагом 0.1 и для каждого временного ряда из пяти (встраиваемая техника, крупная бытовая техника, компьютеры и т.д.) проводилось прогнозирование внутри предыдущего года, то есть для идентификации модели использовались последние 12 значений из 41.
Код перебора в MATLAB выглядит следующим образом.
for alpha = 0 : 0.1 : 1 for gamma = 0 : 0.1 : 1 for delta = 0 : 0.1 : 1 for t = length(TimeSeries(:,1)) - 12 : length(TimeSeries(:,1)) Assessment(q,1) = alpha; Assessment(q,2) = gamma; Assessment(q,3) = delta; Zh(t) = delta * (gamma * (alpha * Z(t-1) + (1-alpha) * Zh(t-1)) + (1-gamma) * Z(t-2)) + (1-delta) * Z(t-12); Assessment(q,4) = Zh(t); Assessment(q,5) = Z(t); end end end end
Здесь переменная Assessment — массив, в котором хранятся результаты вычислений. По итогам приведенных циклов определялись такие значения коэффициентов модели, для которых средняя абсолютная ошибка прогноза (MAE) минимальна.
В итоге для временного ряда продаж встраиваемой техники коэффициенты имеют значение α = 0.2, γ = 0.4, δ = 0.5.
Узкие места экспоненциального сглаживания
На рисунке представлен результат прогнозирования продаж крупной бытовой техники — в этой записи я рассматриваю только один временной ряд. На графике синим цветом показаны фактические значения временного ряда, красным — прогнозные. Мы видим, что временной ряд имеет сложный характер: есть зона временного ряда, на которой происходит постоянное снижение значений, т.е. каждое последующее меньше предыдущего; есть зона, внутри которой значения ряда колеблются относительно постоянной величины (зона стабильности).
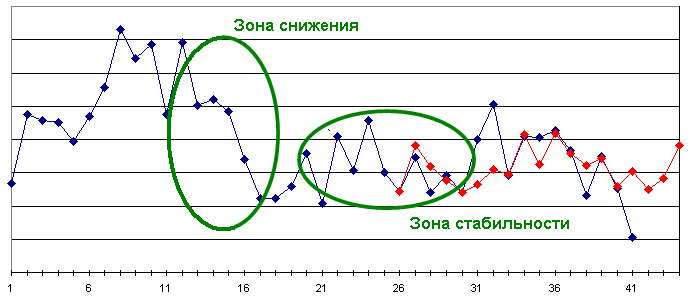
Красным цветом показан прогноз, вычисленный на созданной модели. Мы видим, что в целом «зон колебаний» относительного некоторого среднего значения во временном ряде больше, чем «зон возрастания или снижения». Полученная модель прогнозирования как раз этот нюанс и учитывает — мы видим, что прогноз продолжает колебаться относительно некоторого среднего значения, хотя интуитивно кажется, что снова может наступить «зона снижения» и продажи будут падать. Именно здесь становится очевидным узкое место математической модели прогнозирования, которое состоит в том, что модель не позволяет нам учитывать все тонкости и сложности рассматриваемого временного ряда.
Мы не сможем математически получить такую модель, которая на малом количестве фактических значений временного ряда сможет как «улавливать колебания», так и «переключаться на спады» — модель всегда будет делать что-то одно. Ровно поэтому нам всегда нужна будет экспертная оценка вычисленных прогнозных значений.
Экспертная оценка полученного прогноза
Снова повторю, что, как правило, оценки такого рода прогнозов делают эксперты предметной области, которые годами работают в данной сфере и понимают тонкости не математики, а в первую очередь предметной области, т.е. продаж, тенденций, рынков, инфляций и т.д. Математика в их руках лишь инструмент, который им дает статистические оценки данных, но окончательное прогнозное значение формируют именно эксперты.